Si chiama Plimpton 322 ed è una tavoletta d’argilla scoperta dagli archeologi oltre un secolo fa nel deserto dell’Iraq.
È incisa con caratteri cuneiformi, è antica di almeno 3.600 anni e dimostra che gli scribi delle prime civiltà mesopotamiche applicavano il teorema di Pitagora oltre un millennio prima che Pitagora venisse al mondo.
Tuttavia, quella che può sembrare una “prima pietra” della matematica è in realtà solo la tappa di un lungo viaggio.
Le origini della scienza dei numeri sono infatti molto più remote. Scopriamole insieme.
1. DALLA NATURA AL NUMERO

La capacità di cogliere quella che i neuroscienzati chiamano “numerosità”, ossia una quantità approssimativa più o meno precisa, è innata ed è una facoltà che abbiamo in comune con scimmie, ratti, uccelli e perfino api.
Fin qui la natura. Ma quando e come è avvenuto il passaggio ai numeri veri, ai calcoli e al linguaggio della matematica?
«Esistono società umane nelle cui lingue sono presenti solo i concetti di “uno”, “due” e “molti”», spiega l’astronomo e divulgatore John Barrow (scomparso lo scorso anno) nel suo libro Perché il mondo è matematico? (Laterza).
«E in molte lingue europee gli aggettivi per indicare “primo” e “secondo” non derivano dalle parole “uno” e “due”, mentre “terzo”, “quarto”, e così via, sono chiaramente legati a “tre”, “quattro” e agli altri numeri».
Furono dunque questi concetti astratti (uno, due, molti, pochi) i primi a svilupparsi, sotto la spinta di necessità pratiche. Quali fossero queste necessità e come contassero i nostri antenati lo svelano reperti archeologici precedenti perfino alle tavolette cuneiformi.
«Il metodo di conteggio basato sugli intagli è sicuramente uno dei più antichi», racconta il matematico Bruno D’Amore nel saggio La matematica e la sua storia, scritto con Silvia Sbaraglia.
Il più antico esempio noto si trova su un osso di babbuino rinvenuto nello Swaziland, in Africa (v. foto sotto): ha 37mila anni e qualcuno vi ha inciso 29 tacche.

Secondo Barrow si tratta di un’arma sulla quale il cacciatore teneva il conto degli animali uccisi; per altri era un oggetto legato al ciclo lunare, che è appunto di 29 giorni.
Un manico d’osso inciso e con una punta di quarzo, trovato a Ishango presso il Lago Edoardo, sempre in Africa, è anche più sorprendente: le sue tacche sono raggruppate in modo da ormare una sequenza di numeri primi.
Ma non sappiamo a che cosa servisse, né se gli uomini che lo incisero, a cavallo tra Paleolitico e Neolitico, conoscessero davvero i numeri primi. Accanto alla numerazione per intaglio, c’era quella “di Pollicino”, affidata a sassolini o oggetti analoghi.
Tra le rovine dell’antica città di Nuzi (Iraq) è stato trovato un contenitore di argilla sul quale è inciso un elenco di 48 capi di bestiame: 21 pecore, 6 agnelli femmina, 8 montoni, 6 capre e così via.
Dentro c’erano altrettante palline d’argilla (v. foto sotto). Semplice il principio, praticato ancora oggi in alcune società tradizionali: il pastore che lo ha usato 3mila anni fa aggiungeva una pallina per ogni animale, tenendo così il conto delle sue bestie.

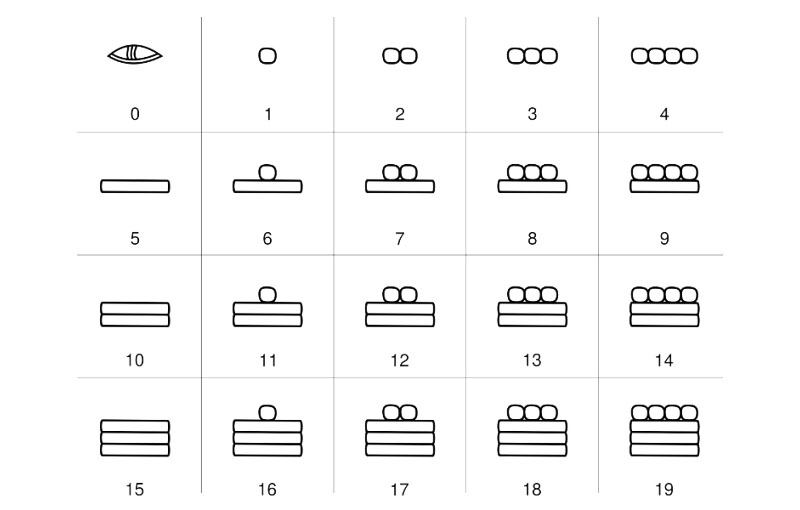
2. DI CHE BASE SEI? POTENZA DI CALCOLO

I sistemi di calcolo dei nostri antenati all’inizio furono probabilmente “a base 2” (come quelli usati ancora oggi dagli aborigeni australiani, che possiedono solo le parole “uno” e “due” per i numeri) oppure a base 5.
Le 55 tacche incise oltre 30mila anni fa su un osso di lupo ritrovato in Moravia (Repubblica Ceca) sono, spiega D’Amore, «uno dei più antichi documenti aritmetici in cui è presente il principio della base di calcolo, dato che le tacche sono raggruppate in gruppi di cinque, come le dita di una mano».
L’uso delle mani (ma anche di falangi, spalle, testa, piedi e così via) come calcolatrici era comune in Mesopotamia, in India, in Cina, tra gli Egizi, i Greci e i Romani.
E questa tecnica ha continuato a tenere banco per tutto il Medioevo, nonostante la diffusione dell’abaco e il successo del Liber abaci (“Il libro del calcolo”) con il quale il matematico e mercante pisano Leonardo Fibonacci nel Duecento diffuse in Europa i numeri arabi.
Dall’altra parte dell’oceano Atlantico, intanto, Maya e Aztechi (v. foto sotto) sviluppavano un sistema a base 20, grazie al quale misero a punto calendari precisi e sofisticati sistemi di misurazione del tempo.
Sumeri e Babilonesi usavano invece una numerazione a base 60 (sessagesimale). Forse derivava da un sistema di pesi e misure comune nell’area, di certo fu favorita da una svolta culturale: la nascita della civiltà urbana in Mesopotamia (ma anche, negli stessi secoli, in Cina e nella Valle dell’Indo), l’accumulo di cereali nei magazzini e una rete dei commerci sempre più estesa richiedevano maggiori capacità di calcolo.
Fu per questo che i Sumeri inventarono appunto l’abaco (noto anche in Estremo Oriente) e, tra 5.300 e 4.500 anni fa, i simboli dei numeri, usati per compilare elenchi di merci, liste di rifornimenti per gli eserciti, contratti di compravendita.
«Risale ai Sumeri anche il primo sistema posizionale, perfezionato in seguito dagli Indiani», spiega D’Amore. «Al valore di ogni simbolo andava aggiunto quello del simbolo immediatamente successivo, addizionandoli».
In pratica, lo stesso modo di formare i numeri che usiamo noi, che però lo abbiamo adottato nel Medioevo dagli Arabi: una rivoluzione, perché permette di scrivere qualsiasi numero usando pochi segni (nel nostro caso 10, compreso lo zero).
Il sistema sessagesimale ci ha lasciato due eredità importanti: il calcolo del tempo (un minuto di 60 secondi, un’ora di 60 minuti) e quello delle coordinate per la navigazione (ogni grado d’arco si divide in 60 minuti e 60 secondi).

3. ANCHE SOTTO LE PIRAMIDI E LA RIVOLUZIONE GRECA
L’altra “casa dei numeri” del Vicino Oriente era l’Egitto dei faraoni.
Gran parte di quello che sappiamo della matematica egizia viene dai poco più di due metri di lunghezza del Papiro Rhind: un’ottantina di problemi e varie tabelle di operazioni, con relative soluzioni, destinati a scribi o sacerdoti di 4mila anni fa (v. foto sotto).
Gli Egizi usavano un sistema a base 10, ma non posizionale; non conoscevano lo zero e facevano di conto per scopi astrologico-religiosi, per costruire templi e tombe e per misurare terreni agricoli.
Nemmeno loro svilupparono un sistema matematico che andasse oltre le necessità pratiche. Per questo, ci volevano i filosofi greci.

Se i Sumero-Babilonesi sapevano produrre terne pitagoriche, non vuol dire che conoscessero il significato del teorema che quei numeri nascondevano.
Furono i semileggendari matematici greci Talete (VII-VI secolo a.C.) e Pitagora (VI-V secolo a.C.), riprendendo la tradizione mesopotamica e quella egizia, a fornire i primi tasselli del pensiero matematico astratto.
E sarà poi Euclide (IV-III secolo a.C.) a mettere insieme il puzzle nei suoi Elementi, un testo fondamentale per millenni, dove si trova anche la dimostrazione del teorema di Pitagora che oggi si studia a scuola.
Geometria e aritmetica nacquero veramente soltanto allora. In un fazzoletto di terra e mare tra l’Asia Minore (Turchia) e l’Attica, nel giro di tre secoli presero forma il pensiero deduttivo, gli assiomi della geometria, il concetto di infinito, i numeri irrazionali e l’idea che tutto in natura si può misurare.
Verso il 300 a.C. la matematica era la cosa più vicina alla scienza che il mondo avesse mai visto. Sotto, Pitagora nell’affresco La Scuola di Atene di Raffaello, in Vaticano.

4. NUOVI MONDI
Il sapere greco fece da ponte tra gli antichi e i moderni. Passando però dall’India, grazie alle conquiste di Alessandro Magno, che aveva spinto fin là la cultura ellenistica.
«Un’efficace base di calcolo, la notazione posizionale e l’uso dello zero garantiscono un sistema di numerazione di successo», spiega Barrow. «E nella storia antica, questi tre elementi si ritrovarono insieme solo in India».
I sapienti hindu, partendo dalle conoscenze ellenistiche, perfezionarono il sistema decimale posizionale, che giungerà in Europa nel Duecento attraverso gli Arabi e grazie, ancora una volta, a Fibonacci.

Ci fu qualche resistenza: la Chiesa tentò inizialmente di vietare l’uso dei numeri “pagani” e del demoniaco zero. Ma presto in Occidente si tornò a osservare il mondo con gli occhi della matematica, come già avevano fatto Talete, Pitagora, Euclide e gli alessandrini.
Le conseguenze furono epocali: la teoria musicale scoprì i rapporti matematici tra i suoni, individuati già da Pitagora; l’economia medievale svoltò grazie alle cifre arabe, che aprirono la strada alla partita doppia e alle banche; la riscoperta degli antichi trattati ellenistici dal ’400 portò i geografi a misurare il Pianeta, i navigatori a raggiungere nuove terre, gli astronomi a comprendere i moti celesti.
Finalmente, la scienza riuscì a darsi un metodo con Galileo Galilei (1564-1642): un uomo per il quale il “grandissimo libro” dell’universo e della natura è scritto “in lingua matematica”, cioè con i numeri.
Sotto, il quadro Il cambiavalute e sua moglie del pittore fiammingo Quentin Metsys, al Louvre di Parigi.

5. LA TAVOLETTA DEI MISTERI

È larga appena 13 centimetri e alta 9, ma per la storia della matematica è più importante delle piramidi egizie.
È la tavoletta Plimpton 322 (v. foto sotto), proveniente dell’antica città di Larsa (Iraq), datata al 1900-1600 a.C. e chiamata così in onore di George Arthur Plimpton (1855-1936), editore e collezionista americano che la donò alla Columbia University di New York.
I suoi segni cuneiformi, decifrati a metà del Novecento, nascondono elenchi di “terne pitagoriche”, ossia sequenze di tre numeri risultanti dall’applicazione di quello che oggi chiamiamo teorema di Pitagora.
Il matematico Daniel F. Mansfield della University of New South Wales di Sydney (Australia) nel 2017 ha ipotizzato che si tratti di tabelle trigonometriche e recentemente ha pubblicato sulla rivista Foundations of Science un nuovo studio sul loro scopo.
«In genere si considera la tavoletta una lista di calcoli scolastici, una sorta di eserciziario per scribi», spiega Mansfield. «Ma questa nuova analisi suggerisce che si tratti invece di uno specifico problema geometrico».
Sarebbe la descrizione di una serie di aree rettangolari con lati uguali. «Questo studio “proto-trigonometrico” non ha nulla a che vedere con la trigonometria sviluppata poi dai Greci osservando il cielo», conclude Mansfield.
«Sembra infatti essere nato dalla necessità di misurare il terreno». Forse per una compravendita, forse per fornire uno strumento di calcolo agli agrimensori mesopotamici.






